Abstract
Brief Communication
Hybridizing intra and extra perspectives in infectious disease modeling
Ruffin-Benoît M Ngoie*
Published: 17 February, 2023 | Volume 4 - Issue 1 | Pages: 004-006
The last four decades have been particularly marked by devastating diseases. During this period, humanity has
experienced plagues such as SARS, bird Flu, Ebola, Chikun-gunya, COVID-19 in addition to diseases that were already decimating populations.
Read Full Article HTML DOI: 10.29328/journal.jcmhs.1001026 Cite this Article Read Full Article PDF
References
- Bernoulli D. Essai d’une nouvelle analyse de la mortalité causée par la petite vérole, et des avantages de l’inoculation pour la prévenir. Histoire de l’Académie royale des sciences: mémoires de mathématiques et de physique. 1766; 1–40.
- Valleron AJ. Les rôles de la modélisation en épidémiologie. Comptes rendus de l’Académie des sciences. Série III, Sciences de la vie. 2000; 323: 5:429-433.
- Kasereka SK, Zohinga GN, Kiketa VM, Ngoie RBM, Mputu EK, Kasoro NM, Kyandoghere K. Equation-Based Modeling vs. Agent-Based Modeling with Applications to the Spread of COVID-19 Outbreak. Mathematics. 2023; 11:253. https://doi.org/10.3390/math11010253
- Ndondo AM, Kasereka SK, Bisuta SF, Kyamakya K, Doungmo EFG, Ngoie RBM. Analysis, modeling and optimal control of COVID-19 outbreak with three forms of infection in the Democratic Republic of the Congo. Results Phys 2021; 24:104096.
- Kasereka S, Kasoro N, Chokki AP. A hybrid model for modeling the spread of epidemics: Theory and simulation, in. In: SKO-Maghreb: Concepts and Tools for knowledge Management (ISKO-Maghreb). 2014 4th International Symposium. IEEE; 2014; 1-7.
- Kasereka S, Le Strat Y, Léon L. Estimation of infection force of hepatitis c virus among drug users in france. In: Recent Advances in Nonlinear Dynamics and Synchronization. Springer. 2018; 319-344.
- Ndondo A, Munganga J, Mwambakana J, Saad-Roy C, Van den Driessche P, Walo R. Analysis of a model of gambiense sleeping sickness in humans and cattle. J Biological Dyn. 2016: 10:347-65.
- Goufo EFD, Maritz R, Munganga J. Some properties of the kermack-mckendrick epidemic model with fractional derivative and nonlinear incidence. Adv Diff Eq. 2014; 2014:278.
- Ndondo AM, Walo RO, Vala-Kisisa MY. Optimal control of a model of gambiense sleeping sickness in humans and cattle, American. J Appl Math. 2016: 4:204-216.
- Kasereka S, Goufo EFD, Tuong VH. Analysis and simulation of a mathematical model of tuberculosis transmission in democratic republic of the congo. Adv Diff Eq. 2020: 642:1-19.
- Kasereka S, Goufo EFD, Tuong VH, Kyamakya K. A stochastic agent-based model and simulation for controlling the spread of tuberculosis in a mixed population structure. In: Developments of Artificial Intelligence Technologies in Computation and Robotics, Prodeedings of the 14th International FLINS Conference (FLINS 2020), Cologne, Germany, 188-21 August 2020, World Scientific, 2020; 659-666.
- Redhwan SS, Abdo MS, Shah K, Abdeljawad T, Dawood S, Abdo HA, Shaikh SL. Mathematical modeling for the outbreak of the coronavirus (COVID-19) under fractional nonlocal operator. Results Phys. 2020; 19:103610.
- Din RU, Shah K, Ahmad I, Abdeljawad T. Study of transmission dynamics of novel COVID-19 by using mathematical model. Adv Diff Eq. 2020; 2020: 1-13.
- Zhang Z, Zeb A, Hussain S, Alzahrani E. Dynamics of COVID-19 mathematical model with stochastic perturbation. Adv Diff Eq. 2020; 2020: 1-12.
- Din RU, Seadawy AR, Shah K, Ullah A, Baleanu D. Study of global dynamics of COVID-19 via a new mathematical model. Results Phys. 2020; 19:103468.
- Tracy M, Cerdá M, Keyes KM. Agent based modeling in public health: Current applications and future directions. Annu Rev Public Health. 2018; 39:77-94.
- Kasereka S, Goufo EFD, Tuong VH. Analysis and simulation of a mathematical model of tuberculosis transmission in democratic republic of the congo. Adv Diff Eq. 2020: 642:1-19.
- Chitnis N, Cushing JM, Hyman JM. Bifurcation analysis of a mathematical model for malaria transmission. SIAM J Appl Math. 2006; 67:24-25.
Figures:
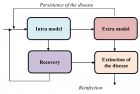
Figure 1
Similar Articles
-
Rural adolescent health: Issues, behaviors and self-reported awarenessMolly Jacobs*. Rural adolescent health: Issues, behaviors and self-reported awareness. . 2020 doi: 10.29328/journal.jcmhs.1001001; 1: 001-017
-
The role of islamic lifestyle and healthy nutrition in accordance with the recommendations of islam and the holly quran by focusing on the risk of cancer incidentRoya Dolatkhah*,Pooneh Jabbaripour,Mohammad Hossein Somi,Ali Roshani. The role of islamic lifestyle and healthy nutrition in accordance with the recommendations of islam and the holly quran by focusing on the risk of cancer incident. . 2020 doi: 10.29328/journal.jcmhs.1001002; 1: 018-022
-
How the COVID-19 outbreak affected physician-patient relationshipRoya Dolatkhah*,Ali Fakhari,Keivan Fakhari Dehkharghani. How the COVID-19 outbreak affected physician-patient relationship. . 2020 doi: 10.29328/journal.jcmhs.1001003; 1: 023-025
-
Assessment of knowledge, practice and associated factors towards prevention of novel corona virus among clients attending at Debre Tabor General Hospital, Debre Tabor Town, North West Ethiopia, 2020: Institutional based cross-sectional studyTigabu Desie Emiru*,Tekalign Amera Birlie,Sheganew Fetene Tasew,Abraham Tsedalu Amare,Nigusie Selomon Tibebu,Chalie Marew Tiruneh. Assessment of knowledge, practice and associated factors towards prevention of novel corona virus among clients attending at Debre Tabor General Hospital, Debre Tabor Town, North West Ethiopia, 2020: Institutional based cross-sectional study. . 2020 doi: 10.29328/journal.jcmhs.1001004; 1: 026-034
-
Utilization of midwives service scheme among women farmers in Southwestern NigeriaOluwasusi JO*,Thomas KA,Olujide MG,Oluwasusi YO. Utilization of midwives service scheme among women farmers in Southwestern Nigeria. . 2020 doi: 10.29328/journal.jcmhs.1001005; 1: 035-046
-
Facing biological risk in child and adolescence neuropsychiatric services during COVID-19 outbreak: Management of protection levels for the direct accessMaria L Tossali*,Carlo Di Brina,Morena Tafuro,Marco Marcelli,Teresa Sebastiani. Facing biological risk in child and adolescence neuropsychiatric services during COVID-19 outbreak: Management of protection levels for the direct access. . 2020 doi: 10.29328/journal.jcmhs.1001006; 1: 047-048
-
Suicide in teenagers during the COVID-19 pandemic in Cuba: actions for its preventionMaydell Pérez Inerárity*,Claudia Elvira Casamayor Leiza,Julio César Pérez Yero,Brayan Chávez Miguel. Suicide in teenagers during the COVID-19 pandemic in Cuba: actions for its prevention. . 2021 doi: 10.29328/journal.jcmhs.1001007; 2: 001-006
-
Institutional capacity of health care institutes for diagnosis and management of common genetic diseases - A study from a north coastal district of Andhra PradeshKoteswara Rao Pagolu*,T Raghava Rao. Institutional capacity of health care institutes for diagnosis and management of common genetic diseases - A study from a north coastal district of Andhra Pradesh. . 2021 doi: 10.29328/journal.jcmhs.1001008; 2: 007-013
-
Neo communicable disease rather than ‘non’ communicable disease for the acronym “NCD”APR Aluwihare*. Neo communicable disease rather than ‘non’ communicable disease for the acronym “NCD”. . 2021 doi: 10.29328/journal.jcmhs.1001009; 2: 014-014
-
Epidemiological profile of the homeless population assisted by voluntary initiative and the social impact on access to healthcare: an investigative study in Curitiba, BrazilFrancelise Bridi Cavassin*,Rafael Senff Gomes,Luiza Cardoso de Lima Passoni,Ricardo Sirigatti. Epidemiological profile of the homeless population assisted by voluntary initiative and the social impact on access to healthcare: an investigative study in Curitiba, Brazil. . 2021 doi: 10.29328/journal.jcmhs.1001010; 2: 015-020
Recently Viewed
-
Non-surgical Treatment of Verrucous Hyperplasia on Amputation Stump: A Case Report and Literature ReviewSajeda Alnabelsi*, Reem Hasan, Hussein Abdallah, Suzan Qattini. Non-surgical Treatment of Verrucous Hyperplasia on Amputation Stump: A Case Report and Literature Review. Ann Dermatol Res. 2024: doi: 10.29328/journal.adr.1001034; 8: 015-017
-
Outpatient operative hysteroscopy: evaluation of patient satisfaction and acceptanceClare Margaret Crowley*,Noelle Gill,Minna Geisler. Outpatient operative hysteroscopy: evaluation of patient satisfaction and acceptance. Clin J Obstet Gynecol. 2022: doi: 10.29328/journal.cjog.1001098; 5: 005-008
-
Predictors of positive treatment response to PTNS in women with overactive bladderSuneetha Rachaneni*,Doyo Enki,Megan Welstand,Thomasin Heggie,Anupreet Dua. Predictors of positive treatment response to PTNS in women with overactive bladder. Clin J Obstet Gynecol. 2022: doi: 10.29328/journal.cjog.1001097; 5: 001-004
-
Prediction of neonatal and maternal index based on development and population indicators: a global ecological studySedigheh Abdollahpour,Hamid Heidarian Miri,Talat Khadivzadeh*. Prediction of neonatal and maternal index based on development and population indicators: a global ecological study. Clin J Obstet Gynecol. 2021: doi: 10.29328/journal.cjog.1001096; 4: 101-105
-
A Genetic study in assisted reproduction and the risk of congenital anomaliesKaparelioti Chrysoula,Koniari Eleni*,Efthymiou Vasiliki,Loutradis Dimitrios,Chrousos George,Fryssira Eleni. A Genetic study in assisted reproduction and the risk of congenital anomalies. Clin J Obstet Gynecol. 2021: doi: 10.29328/journal.cjog.1001095; 4: 096-100
Most Viewed
-
Evaluation of Biostimulants Based on Recovered Protein Hydrolysates from Animal By-products as Plant Growth EnhancersH Pérez-Aguilar*, M Lacruz-Asaro, F Arán-Ais. Evaluation of Biostimulants Based on Recovered Protein Hydrolysates from Animal By-products as Plant Growth Enhancers. J Plant Sci Phytopathol. 2023 doi: 10.29328/journal.jpsp.1001104; 7: 042-047
-
Sinonasal Myxoma Extending into the Orbit in a 4-Year Old: A Case PresentationJulian A Purrinos*, Ramzi Younis. Sinonasal Myxoma Extending into the Orbit in a 4-Year Old: A Case Presentation. Arch Case Rep. 2024 doi: 10.29328/journal.acr.1001099; 8: 075-077
-
Feasibility study of magnetic sensing for detecting single-neuron action potentialsDenis Tonini,Kai Wu,Renata Saha,Jian-Ping Wang*. Feasibility study of magnetic sensing for detecting single-neuron action potentials. Ann Biomed Sci Eng. 2022 doi: 10.29328/journal.abse.1001018; 6: 019-029
-
Pediatric Dysgerminoma: Unveiling a Rare Ovarian TumorFaten Limaiem*, Khalil Saffar, Ahmed Halouani. Pediatric Dysgerminoma: Unveiling a Rare Ovarian Tumor. Arch Case Rep. 2024 doi: 10.29328/journal.acr.1001087; 8: 010-013
-
Physical activity can change the physiological and psychological circumstances during COVID-19 pandemic: A narrative reviewKhashayar Maroufi*. Physical activity can change the physiological and psychological circumstances during COVID-19 pandemic: A narrative review. J Sports Med Ther. 2021 doi: 10.29328/journal.jsmt.1001051; 6: 001-007

HSPI: We're glad you're here. Please click "create a new Query" if you are a new visitor to our website and need further information from us.
If you are already a member of our network and need to keep track of any developments regarding a question you have already submitted, click "take me to my Query."